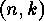 -codes. Let
-codes. Let  be a linear
be a linear
 -code over
-code over 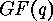 with generator matrix
with generator matrix  and let
and let  be a linear
be a linear  -code over
-code over 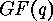 with generator matrix
with generator matrix  ,
then the code
,
then the code  with generator matrix
with generator matrix
In order to minimize the number of orbits that must be enumerated or
represented, and following SLEPIAN again, we can restrict attention to
indecomposable linear 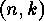 -codes. Let
-codes. Let  be a linear
be a linear
 -code over
-code over 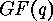 with generator matrix
with generator matrix  and let
and let  be a linear
be a linear  -code over
-code over 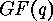 with generator matrix
with generator matrix  ,
then the code
,
then the code  with generator matrix
with generator matrix

is called the direct sum of the codes  and
and  , and it will be
denoted by
, and it will be
denoted by  . A code
. A code  is called decomposable, if
and only if it is equivalent to a code which is the direct sum of two or more
linear codes. Otherwise it is called indecomposable.
is called decomposable, if
and only if it is equivalent to a code which is the direct sum of two or more
linear codes. Otherwise it is called indecomposable.
Since there are some errors in
SLEPIAN's table of the numbers of isometry classes
of indecomposable 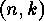 -codes, denoted by
-codes, denoted by  or
or  ,
the following theorem is proved in [5]:
,
the following theorem is proved in [5]:
This formula is implemented in SYMMETRICA as well. For instance for computing
the tables of  and
and  one can use the next program:
one can use the next program:
INT co_all_codes()
{
OP n,k,q,R,S;
INT i,j;
INT erg=OK;
n=callocobject();
k=callocobject();
q=callocobject();
S=callocobject();
R=callocobject();
erg+=printeingabe("maximum value of n=? ");
erg+=scan(INTEGER,n);
erg+=printeingabe("maximum value of k=? ");
erg+=scan(INTEGER,k);
erg+=printeingabe("q=? ");
erg+=scan(INTEGER,q);
erg+=all_codes(n,k,q,S,R);
erg+=println(S);
erg+=println(R);
erg+=freeall(n); erg+=freeall(k); erg+=freeall(q);
erg+=freeall(S); erg+=freeall(R);
if (erg!=OK) return error(" in computation of co_all_codes");
return erg;
}
The routine all_codes(n,k,q,S,R) first computes the numbers
 for
for  and
and  by (1),
then the
by (1),
then the  by (2) and
finally the
by (2) and
finally the  by (5). For computing the numbers of
classes of injective linear
by (5). For computing the numbers of
classes of injective linear 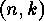 -codes by (3), (4) and (5)
there is the routine
-codes by (3), (4) and (5)
there is the routine all_inj_codes(n,k,q,S,R).
The following tables
for  ,
,  and
and  were computed using these two routines:
were computed using these two routines:
Table 1: Number of isometry classes of linear 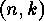 -codes over
-codes over 

Table 2: Number of isometry classes of indecomposable linear
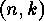 -codes over
-codes over 

Table 3: Number of isometry classes of injective linear 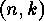 -codes over
-codes over


Table 4: Number of isometry classes of injective
indecomposable linear 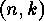 -codes over
-codes over 

In [5] there are tables of  and
and  for
for  . Tables of
. Tables of  can be found in [4][3]
and in the article of WILD [12], when interpreting matroids
as linear codes.
Extensions of the tables given in
[11] for the binary case were evaluated by LATTERMANN in
[10].
can be found in [4][3]
and in the article of WILD [12], when interpreting matroids
as linear codes.
Extensions of the tables given in
[11] for the binary case were evaluated by LATTERMANN in
[10].
In her thesis [1],
ARNOLD evaluated transversals of isometry classes of linear codes. Another
implementation, due to BETTEN allowed to evaluate representatives of
all the isometry classes of indecomposable binary 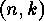 -codes for
-codes for  except for the case of
except for the case of  and
and  . Use was made of orderly generation
in connection with isomorphism checking [2].
Details will be given elsewhere.
. Use was made of orderly generation
in connection with isomorphism checking [2].
Details will be given elsewhere.