Isometry classes of linear codes



Next: Indecomposable codes
Up:
Enumeration of isometry-classes
Previous:
Enumeration of isometry-classes
A linear 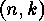 -code over the Galois field
-code over the Galois field 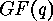 is a
is a
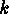 -dimensional subspace of the vector space
-dimensional subspace of the vector space 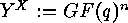 ,
where
,
where 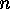 denotes the set
denotes the set 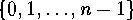 . As usual
codewords will be written as rows
. As usual
codewords will be written as rows 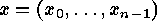 . A
. A 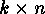 -matrix
-matrix 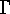 over
over 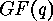 is called a generator matrix of the
linear
is called a generator matrix of the
linear 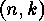 -code
-code  , if and only if the rows of
, if and only if the rows of 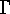 form a basis of
form a basis of
 , so that
, so that 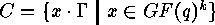 . Two linear
. Two linear
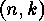 -codes
-codes 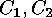 are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps
are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps  onto
onto
 . Using the notion of finite group actions (see [8])
one can easily express
equivalence of codes in terms of the wreath product action:
. Using the notion of finite group actions (see [8])
one can easily express
equivalence of codes in terms of the wreath product action:
 and
and  are equivalent, if and only if there exist
are equivalent, if and only if there exist 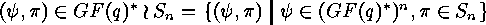 (where
(where 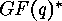 denotes the multiplicative group of the
Galois field) such that
denotes the multiplicative group of the
Galois field) such that 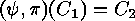 .
.
The complete monomial group 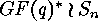 of degree
of degree 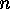 over
over
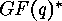 acts on
acts on 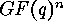 by the following definition:
by the following definition:

In order to apply the results of the theory of finite group actions, this
equivalence relation for linear 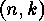 -codes is translated into an
equivalence relation for generator matrices of linear codes, and these
generator matrices are considered to be functions
-codes is translated into an
equivalence relation for generator matrices of linear codes, and these
generator matrices are considered to be functions 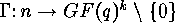 where
where 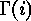 is the
is the 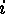 -th column of the
generator matrix
-th column of the
generator matrix 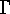 . (We exclude
. (We exclude  -columns for obvious reasons.)
-columns for obvious reasons.)
As a generalization of SLEPIAN's article [11]
we show in [5] that, by using LEHMANN's Lemma about
actions of the wreath product, the generating function for the numbers
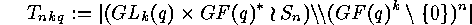
can be computed by the following substitution into the cycle index of the
projective group 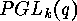 acting on the
acting on the  -dimensional projective space
-dimensional projective space  :
:
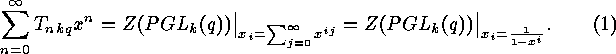
Since the 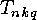 can be interpreted as numbers of classes of
can be interpreted as numbers of classes of
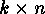 -matrices
of rank
-matrices
of rank 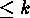 the numbers
the numbers  , which are the numbers of isometry
classes of linear
, which are the numbers of isometry
classes of linear 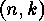 -codes with no columns of zeros, satisfy
-codes with no columns of zeros, satisfy
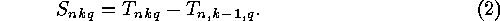
Restricting our attention to codes with generator matrices  , such that
, such that
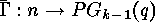 ,
, 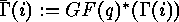 is
injective, we can derive the
numbers of isometry classes of "injective" linear codes, obtaining
is
injective, we can derive the
numbers of isometry classes of "injective" linear codes, obtaining
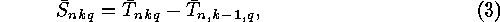
where the 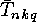 are computed by:
are computed by:
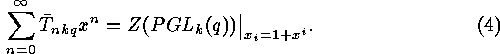
In [3] it is shown how the cycle index of 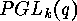 acting
on
acting
on 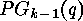 can be computed. This paper is a generalization of [11]
and of HARRISON [6][7], where the cycle indices
of
can be computed. This paper is a generalization of [11]
and of HARRISON [6][7], where the cycle indices
of 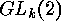 are computed.
The idea for computing these cycle indices is the
following: First determine the conjugacy classes in
are computed.
The idea for computing these cycle indices is the
following: First determine the conjugacy classes in 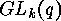 , which can
be done by using the theory of normal forms of matrices. Then determine the
number of elements in these conjugacy classes, for instance by applying a very
nice formula of KUNG [9]. Finally compute the cycle type of
one representative of each class. (It is well known that all elements in one
conjugacy class are of the same cycle type.)
These formulae have been implemented into SYMMETRICA, so a C-program for
computing
, which can
be done by using the theory of normal forms of matrices. Then determine the
number of elements in these conjugacy classes, for instance by applying a very
nice formula of KUNG [9]. Finally compute the cycle type of
one representative of each class. (It is well known that all elements in one
conjugacy class are of the same cycle type.)
These formulae have been implemented into SYMMETRICA, so a C-program for
computing 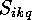 for
for 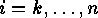 can be written in the following
way:
can be written in the following
way:
INT S_nkq_maxgrad(n,k,q,f)
OP n,k,q,f;
{
OP c,d;
INT erg=OK;
c=callocobject();
d=callocobject();
erg+=T_nkq_maxgrad(n,k,q,c);
if (gt(k,cons_eins))
{
erg+=dec(k);
erg+=T_nkq_maxgrad(n,k,q,d);
erg+=inc(k);
erg+=sub(c,d,f);
}
else erg+=copy(c,f);
erg+=freeall(c);
erg+=freeall(d);
if (erg!=OK) return error(" in computation of S_nkq_maxgrad");
return erg;
}
The program for the computation of the 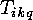 for
for  is the
following:
is the
following:
INT T_nkq_maxgrad(n,k,q,f)
OP k,q,n,f;
{
OP c,d;
INT erg=OK;
c=callocobject();
d=callocobject();
erg+=zykelind_pglkq(k,q,c);
erg+=numberofvariables(c,d);
erg+=co_polya3_sub(c,d,n,f);
erg+=freeall(c);
erg+=freeall(d);
if (erg!=OK) return error(" in computation of T_nkq_maxgrad");
return erg;
}
With the routine zykelind_pglkq(k,q,c) one can compute the cycle index of
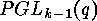 acting on the projective space
acting on the projective space 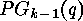 , and the routine
, and the routine
co_polya3_sub(c,d,n,f) computes the first part of degree 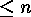 of the substitution
of the substitution 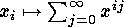 in the polynomial
in the polynomial
c. Both these routines can be found in the source file zykelind.c.



Next: Indecomposable codes
Up:
Enumeration of isometry-classes
Previous:
Enumeration of isometry-classes
Herr Fripertinger
Sun Feb 05 16:50:39 MET 1995
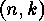 -code over the Galois field
-code over the Galois field 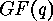 is a
is a
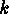 -dimensional subspace of the vector space
-dimensional subspace of the vector space 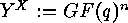 ,
where
,
where 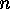 denotes the set
denotes the set 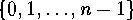 . As usual
codewords will be written as rows
. As usual
codewords will be written as rows 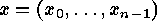 . A
. A 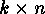 -matrix
-matrix 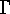 over
over 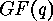 is called a generator matrix of the
linear
is called a generator matrix of the
linear 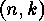 -code
-code  , if and only if the rows of
, if and only if the rows of 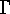 form a basis of
form a basis of
 , so that
, so that 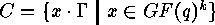 . Two linear
. Two linear
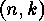 -codes
-codes 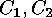 are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps
are called equivalent, if and only if there
is an isometry (with respect to the Hamming metric) which maps  onto
onto
 . Using the notion of finite group actions (see [8])
one can easily express
equivalence of codes in terms of the wreath product action:
. Using the notion of finite group actions (see [8])
one can easily express
equivalence of codes in terms of the wreath product action:
 and
and  are equivalent, if and only if there exist
are equivalent, if and only if there exist 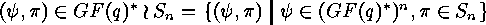 (where
(where 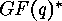 denotes the multiplicative group of the
Galois field) such that
denotes the multiplicative group of the
Galois field) such that 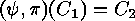 .
.
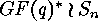 of degree
of degree 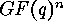 by the following definition:
by the following definition:
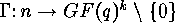 where
where 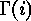 is the
is the 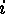 -th column of the
generator matrix
-th column of the
generator matrix  -columns for obvious reasons.)
-columns for obvious reasons.)
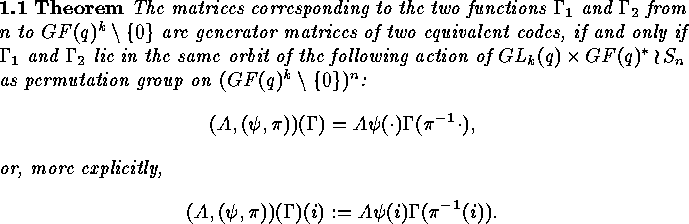
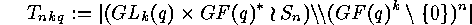
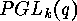 acting on the
acting on the 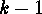 -dimensional projective space
-dimensional projective space 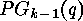 :
:
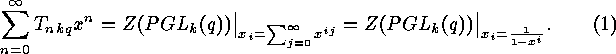
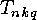 can be interpreted as numbers of classes of
can be interpreted as numbers of classes of
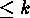 the numbers
the numbers  , which are the numbers of isometry
classes of linear
, which are the numbers of isometry
classes of linear 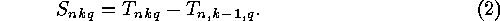
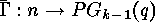 ,
, 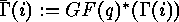 is
injective, we can derive the
numbers of isometry classes of "injective" linear codes, obtaining
is
injective, we can derive the
numbers of isometry classes of "injective" linear codes, obtaining
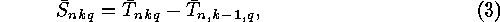
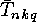 are computed by:
are computed by:
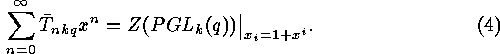
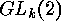 are computed.
The idea for computing these cycle indices is the
following: First determine the conjugacy classes in
are computed.
The idea for computing these cycle indices is the
following: First determine the conjugacy classes in 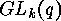 , which can
be done by using the theory of normal forms of matrices. Then determine the
number of elements in these conjugacy classes, for instance by applying a very
nice formula of KUNG
, which can
be done by using the theory of normal forms of matrices. Then determine the
number of elements in these conjugacy classes, for instance by applying a very
nice formula of KUNG 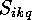 for
for 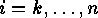 can be written in the following
way:
can be written in the following
way:
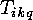 for
for  is the
following:
is the
following:
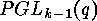 acting on the projective space
acting on the projective space 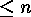 of the substitution
of the substitution 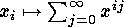 in the polynomial
in the polynomial