The action on the set of vertices

The action on the set of vertices

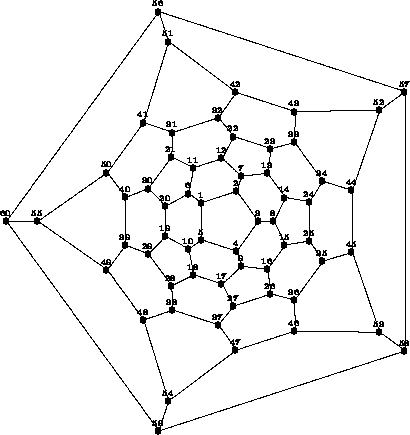
Labelling the vertices of the fullerene C₆₀ as is indicated in figure the permutation representation of generators of R and S acting on the set of vertices is given by:

p₁= (56,57,58,59,60)(51,52,53,54,55)(42,44,46,48,50)(41,43,45,47,49)(32,34,36,38,40) (31,33,35,37,39)(22,24,26,28,30)(21,23,25,27,29)(12,14,16,18,20)(11,13,15,17,19) (6,7,8,9,10)(1,2,3,4,5)

p₂= (37,38,48,54,47)(27,28,49,59,46)(18,39,60,53,26)(17,29,55,58,36)(10,40,56,45,16) (9,19,50,57,35)(7,12,22,23,13)(5,30,51,44,15)(4,20,41,52,25)(3,6,31,43,24) (2,11,32,33,14)(1,21,42,34,8)

s= (58)(57,59)(56,60)(53)(52,54)(51,55)(45,46)(44,47)(43,48)(42,49)(41,50)(35,36) (34,37)(33,38)(32,39)(31,40)(25,26)(24,27)(23,28)(22,29)(21,30)(15,16)(14,17)(13,18) (12,19)(11,20)(8,9)(7,10)(6)(3,4)(2,5)(1)

p₁ is a 5-fold rotation around the centre of figure and p₂ is a 5-fold rotation, where the rotation axis goes through the centres of the faces {7,12,22,23,13} and {37,38,48,54,47} .

There are computer algebra systems which evaluate the cycle index of a permutation group given by a set of generators. For instance the SYMMETRICA routine zykelind_arb(a,b) computes the cycle index b of a permutation group with generators given in the VECTOR-object a. In this way the cycle indices of R and S acting on the set of vertices are computed as

Z(R,Vertices)=(1)/(60)(24 x₅¹² +20 x₃²⁰ +15 x₂³⁰ +x₁⁶⁰)

Z(S,Vertices)=(1)/(120)(24 x₁₀⁶ +20 x₆¹⁰ +24 x₅¹² +20 x₃²⁰ +16 x₂³⁰ +15 x₁⁴ x₂²⁸ +x₁⁶⁰).

The action on the set of vertices