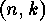Methods for constructing representatives of classes of linear 
-codes
obviously do not reach as far as the enumerative methods, but the use of
computers allows to get a complete overview of linear 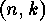-codes over
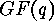for quite a number of parameter triples 
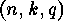. We have seen
before that the isometry classes can be described as orbits of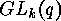 
on
sets of mappings into the projective space. A very interesting and helpful
constructive method for discrete structures which can be defined as orbits of
finite groups on finite sets is based on the following fact. If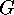 
is a
transitive permutation group on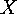 
, then the orbits of a subgroup 
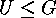on 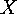can be bijectively mapped onto double cosets as follows: For any 
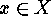the mapping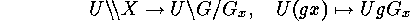
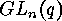is a bijection. In the case of the -codes we can use the fact that the
general linear group 
is transitive on the set 
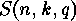of
subspaces of dimensio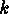n 
in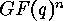 
, so that the isometry classes of
linear -codes turn out to be in one-one-correspondence with the set of
double cosets
where 
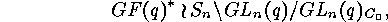
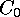is any linear -code. A computer program due to WEINRICH ([14]) allows to evaluate complete sets of
representatives, and it was recently improved by using, besides of double
cosets the combinatorial method of orderly generation. The work in
this field of constructive theory is still in rapid progress, so that we
cannot tell yet how far we can reach.