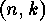 -codes. Let
-codes. Let 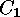 be a linear
be a linear
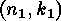 -code over
-code over 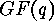 with generator matrix
with generator matrix 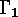 and let
and let 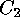 be a linear
be a linear 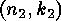 -code over
-code over 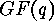 with generator matrix
with generator matrix 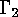 ,
then the code
,
then the code 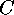 with generator matrix
with generator matrix
In order to minimize the number of orbits that must be enumerated or
represented, and following SLEPIAN again, we can restrict attention to
indecomposable linear 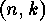 -codes. Let
-codes. Let 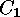 be a linear
be a linear
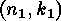 -code over
-code over 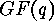 with generator matrix
with generator matrix 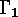 and let
and let 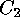 be a linear
be a linear 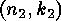 -code over
-code over 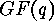 with generator matrix
with generator matrix 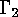 ,
then the code
,
then the code 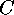 with generator matrix
with generator matrix
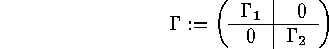
is called the direct sum of the codes 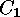 and
and 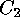 , and it will be
denoted by
, and it will be
denoted by 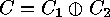 . A code
. A code 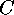 is called decomposable, if
and only if it is equivalent to a code which is the direct sum of two or more
linear codes. Otherwise it is called indecomposable.
is called decomposable, if
and only if it is equivalent to a code which is the direct sum of two or more
linear codes. Otherwise it is called indecomposable.
In [13] SLEPIAN proves that every decomposable linear
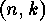 -code is equivalent to a direct sum of indecomposable codes, and that
this decomposition is unique up to equivalence and order of the summands.
SLEPIAN used a generating function scheme for computing the numbers
-code is equivalent to a direct sum of indecomposable codes, and that
this decomposition is unique up to equivalence and order of the summands.
SLEPIAN used a generating function scheme for computing the numbers
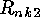 and
and 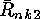 . However after constructing these codes the
authors realized that in some situations this formula doesn't work correctly.
For that reason we are giving another formula to determine the numbers
. However after constructing these codes the
authors realized that in some situations this formula doesn't work correctly.
For that reason we are giving another formula to determine the numbers
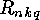 and
and 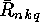 . For the rest of this section let
. For the rest of this section let 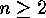 .
.
where
and where the first sum is taken over the cycle types 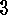 .
.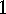 Theorem
The number
Theorem
The number 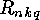 is equal to
is equal to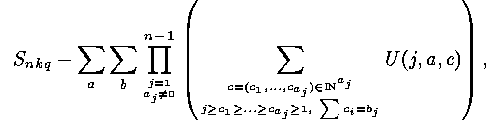
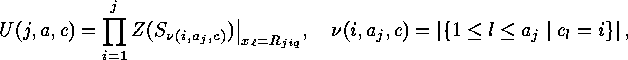
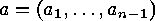 of
of 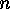 , (which means that
, (which means that 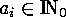 and
and 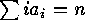 ) such that
) such that 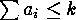 , while the second sum is over the
, while the second sum is over the 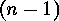 -tuples
-tuples 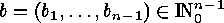 , for which
, for which 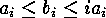 , and
, and
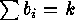 . In the same way the
. In the same way the 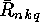 can be computed from the
can be computed from the
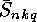 . The numerical results show that for fixed
. The numerical results show that for fixed  and
and 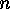 the
sequence of
the
sequence of 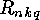 is unimodal and symmetric. (It is easy to prove that
this sequence must be symmetric, but the proof of the unimodality is still
open.)
is unimodal and symmetric. (It is easy to prove that
this sequence must be symmetric, but the proof of the unimodality is still
open.)
Proof:
In order to evaluate the values 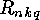 the number of all classes of
decomposable linear
the number of all classes of
decomposable linear 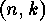 -codes must be subtracted from
-codes must be subtracted from 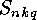 . In other
words one has to find all possibilities of decomposing a linear
. In other
words one has to find all possibilities of decomposing a linear 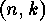 -code
into a direct sum of indecomposable linear
-code
into a direct sum of indecomposable linear 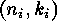 -codes such that
-codes such that
According to SLEPIANs theorem the 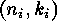 -codes can be arranged
such that
-codes can be arranged
such that 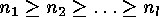 and in the case that
and in the case that 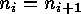 the inequality
the inequality 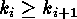 holds. At first all partitions of
holds. At first all partitions of 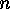 into
at least two parts and into at most
into
at least two parts and into at most 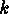 parts must be found. Let
parts must be found. Let
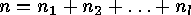 be such a partition with
be such a partition with 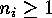 and
and 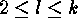 . Then the cycle type of
. Then the cycle type of 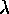 is
is  , where
, where
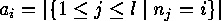 . Two decomposable codes which
determine two different partitions of
. Two decomposable codes which
determine two different partitions of 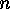 are not equivalent. In the second
step to each partition of
are not equivalent. In the second
step to each partition of 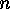 one has to find all sequences
one has to find all sequences  such that
such that 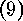 is fulfilled, and such that codes belonging to
different sequences are not equivalent. In order to do this we start with
such a sequence
is fulfilled, and such that codes belonging to
different sequences are not equivalent. In order to do this we start with
such a sequence  and define
and define

then
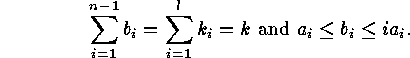
Two decomposable codes which on the one hand belong to one partition of 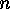 but on the other hand define two different vectors
but on the other hand define two different vectors 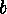 and
and 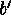 are not in
the same equivalence class. Now the other way round we start with a sequence
are not in
the same equivalence class. Now the other way round we start with a sequence
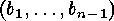 and try to determine all sequences
and try to determine all sequences  which define non equivalent codes such that
which define non equivalent codes such that 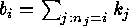 .
Again by SLEPIAN's theorem we must find all partitions of
.
Again by SLEPIAN's theorem we must find all partitions of 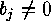 (this implies
(this implies 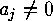 ) into exacyly
) into exacyly 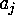 parts of the form
parts of the form
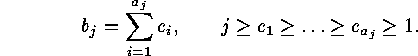
In the last step 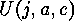 must be evaluated. This is the the number of
classes of linear
must be evaluated. This is the the number of
classes of linear 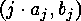 -codes, which have a decomposition into a
direct sum of indecomposable
-codes, which have a decomposition into a
direct sum of indecomposable 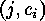 -codes for
-codes for 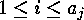 to a
given partition
to a
given partition  of
of 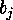 into exactly
into exactly 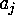 parts. We already know that there are
parts. We already know that there are
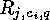 classes of indecomposable linear
classes of indecomposable linear 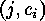 -codes. In the case
that all the
-codes. In the case
that all the 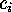 are distinct, this number is given by
are distinct, this number is given by

Otherwise there exist 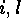 such that
such that 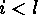 and
and 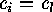 . Then
. Then
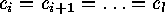 and permuting the corresponding summands in the
direct sum may lead to equivalent codes. For
and permuting the corresponding summands in the
direct sum may lead to equivalent codes. For 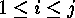 let
let
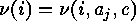 be the cardinality of
be the cardinality of 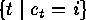 . Now there
is a bijection between the classes of codes, which are a direct sum of
. Now there
is a bijection between the classes of codes, which are a direct sum of
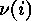
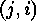 -codes and the orbits of the symmetric group
-codes and the orbits of the symmetric group 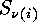 on the set of all mappings from
on the set of all mappings from 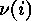 into a set of
into a set of 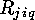 elements,
where the action of
elements,
where the action of 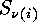 is given by:
is given by:
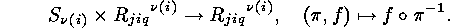
By PÓLYAs theorem [12] one has to compute the cycle index
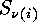 and each variable must be substituted by
and each variable must be substituted by 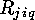 . Doing
this for all possible values of
. Doing
this for all possible values of 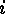 we get
we get
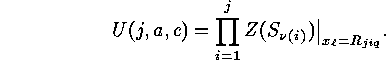
Using the computer algebra system SYMMETRICA, among many other ones the tables of numbers of indecomposable codes which are shown below were computed.