Prof. Dr. R. Laue
WS9900
Informatik I
Übungsblatt 5
Abgabe: 14.12.99 vor der Vorlesung
URL: /axel/informatik1_ws9900_blatt5.html
Dieses Übungsblatt ist in Zweiergruppen zu bearbeiten.
Auf dem Blatt bitte den Übungsgruppentag angeben. Um den Übungsschein
zu erhalten, muß man 50% der Punkte erreichen und zweimal erfolgreich
eine Aufgabe vorrechnen.
Aufgabe 13 - Boole´sche Algebra - (3 Punkte)
Gibt es eine Boole'´sche Algebra (M,+,.,-) mit genau
drei Elementen? Beweis!
Aufgabe 14 - Boole´sche Algebra - (3 Punkte)
Zeigen Sie, daß für jede Menge X, das Tupel (P(X),  ,
,  ,-)
eine Boole´ sche Algebra ist. Wobei
,-)
eine Boole´ sche Algebra ist. Wobei
P(X) := { Y | Y 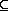 X }
X }
_
Y := { x 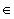 X | x
X | x 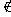 Y}
Y} 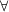 Y
Y 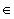 P(X)
P(X)
und die Vereinigung der Operation + und die Schnittbildung
der Operation
. entspricht. Welche Mengen sind 0 und 1 der Algebra?
Aufgabe 15 - Gatter - ( 3+1+3+2 Punkte)
Wir wollen zusätzlich zu den NICHT ODER UND Gattern
noch NAND EXOR und Halbaddierer kennenlernen:
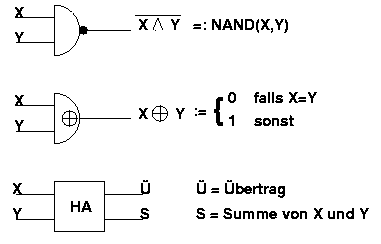 a) Drücken Sie NICHT ODER UND mittels NAND aus.
b) Drücken Sie EXOR mittels NICHT ODER UND aus.
c) Stellen Sie EXOR mittels vier NAND Gatter dar und zeichen
Sie das Schlatnetz.
d) Drücken Sie S und Ü des Halbaddierers mit EXOR
und UND aus. Zeichnen Sie das Schaltnetz.
a) Drücken Sie NICHT ODER UND mittels NAND aus.
b) Drücken Sie EXOR mittels NICHT ODER UND aus.
c) Stellen Sie EXOR mittels vier NAND Gatter dar und zeichen
Sie das Schlatnetz.
d) Drücken Sie S und Ü des Halbaddierers mit EXOR
und UND aus. Zeichnen Sie das Schaltnetz.
Aufgabe 16 - Addierer - (4 Punkte)
Wir wollen zwei zweistellige Dualzahlen a = a0
+ a1.2 und b = b0 + b1.2
multiplizieren:
ab = :c = c0 + c1.2
+ c2.22 +c3 .23
Entwerfen Sie ein Schaltnetz bestehend aus zwei Halbaddiern
und 4 UND Gattern, das die ai bi als Eingänge
(4 Stück) und die ci als Ausgänge besitzt. Begründung.
