Prof. Dr. R.
Laue
Dr. A. Kohnert
Diskrete Algorithmen
SS2005
Übungsblatt 9
Besprechung 24.6.05
URL: /axel/disc_ss05_blatt9.html
Abgabe zu Beginn der Übung.
Aufgabe 16- Ford Fulkerson (5 Punkte)
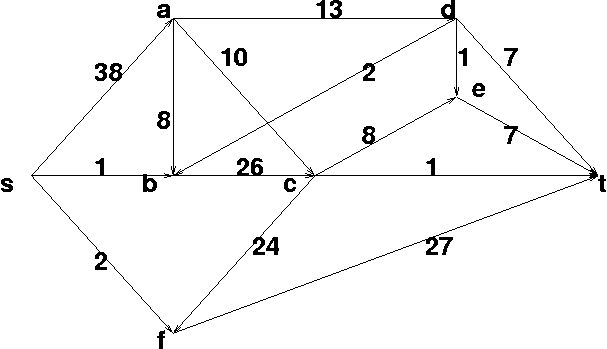
Berechne für folgendes Netzwerk den maximalen Fluss von s nach t
nach dem Algorithmus von Edmonds und Karp. Jeden einzelnen Fluss bitte
einzeichnen.
Am Ende einen minimalen Schnitt noch einzeichnen.
Aufgabe 17 - Ärzte
Notdienst (5
Punkte)
In einem Krankenhaus arbeiten n Ärzte. Es geht um die
Belegung von k Feiertagszeiten D1,...., Dk
unterschiedlicher Länge (ein einzelner Feiertag oder aber
Weihnachten mit mehreren Tagen). Für jeden Arzt gibt es
Feiertagsmengen S1,...,Sn an denen er
verfügbar ist. (Dies kann auch nur einzelne Tage aus den Di
umfassen, z.B. nur am 1. Weihnachsfeiertag). Finden Sie einen
polynomialen Algorithmus der entscheidet ob bei gegebenen Di
und Si eine Lösung möglich ist, d.h. für
jeden Tag ist ein Arzt da. Dabei ist zu beachten, dass jeder Arzt nur
an maximal c Tagen im Jahr Notdienst haben soll. Ferner
soll er auch nur an höchstens einem Tag einer Feiertagsperiode
Dienst haben.
Hinweis: nicht umsonst ist diese Aufgabe auf
einem Netzwerkübungsblatt.
