Prof. Dr. R. Laue                                                                            SS2005
Dr. A. Kohnert
                                Diskrete Algorithmen
                                Übungsblatt 6
                                Besprechung 3.6.05

URL:         /axel/disc_ss05_blatt6.html

Abgabe zu Beginn der Übung.

Aufgabe 10  stark zusammenhängend (4 Punkte)


Führen Sie am folgenden Beispiel die Berechnung der starken Zusammenhangskomponenten durch.

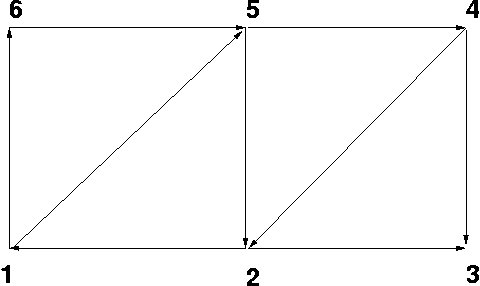
graph
Starten Sie am Knoten 1. Stellen Sie den jeweiligen Kellerinhalt dar.Wie sind die Belegungen von LOWPT,DFSNUM,CURRENT und S?

Aufgabe 11 bcc Teil 1 (4 Punkte)


Ein ungerichteter Graph G=(V,E) heißt zweifach zusammenhängend, wenn G\v für jeden Knoten v aus V zusammenhängend ist. Eine Zweifachzusammenhangskomponente (bcc) ist ein maximaler zweifach zusammenhängender Teilgraph.

Beweisen Sie folgendes Lemma:
Seien G1=(V1,E1) .... Gm=(Vm,Em) die bcc des Graphen G=(V,E). Dann bilden die Kantenmengen E1, ..., Em eine Partition von E, d.h. sie sind paarweise disjunkt und die Vereinigung ist E.