| The group action both on the domain and on the range of functions |
G´(H\\YX) -> H\\YX, (g,H(f)) -> H(f o g-1).In order to compute all G´H-orbits on YX we have to adapt the algorithm for computing all G-orbits on YX. Again we write the elements in YX as vectors in mn such that we can choose the lexicographically smallest element of an orbit as its canonic representative. The list of all possible representatives, which must be tested to be the smallest elements in their orbits, is given by the transversal T(H\\YX) of canonic representatives of H-orbits on YX computed above. When doing the minimality test for the orbit H(f) given by its canonic representative f, for all gÎG we first have to compute f o g. Then we must determine the canonic representative [~f] of the orbit H(f o g). If [~f] <f then f is not the canonic representative of the orbit (G´H)(f). Only in those cases when f is less than or equal to the canonic representatives of H(f o g) for all gÎG, the function f is the canonic representative of its G´H-orbit. (For the rest of this paragraph we will not distinguish between the orbit H(f) and its canonic representative, which will be indicated as H(f) as well.) For doing this minimality test it is convenient to know strong generators (the so called Sims-chain) of the group G. In certain cases we don't have to compute and apply all group elements, but we can make jumps and leave some parts of the tree (holding all elements of G, built from its generators) out, which will be described next.
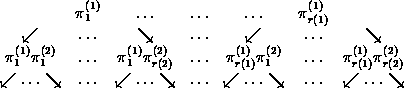
Let CG(i) be the pointwise stabilizer of {1,...,i} in G and let
{pj(i)|1£i£n, 1£j£r(i))}be the strong generators of G such that
CG(i-1)=Èj=1r(i)pj(i)CG(i), where p1(i)ÎCG(i),then we have:
Again we can restrict this group action to an action on the set of all injective functions, which leads to the determination of double-coset representatives H\Sn/G in the case n=m. This algorithm works for arbitrary groups G and H. In the case when H is a Young group or a wreath product you should apply special routines using the so called Leiterspiel, implemented by Schmalz [19], Weinrich [21] and Betten [1], which are much faster in these situations.
| The group action both on the domain and on the range of functions |