Cycle decomposition
The points which form the first row need not be written in their natural order,
e.g.
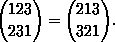 Keeping this in mind, we call a permutation pÎSn a cyclic
permutation or a cycle if and only if it can be written
in the form
Keeping this in mind, we call a permutation pÎSn a cyclic
permutation or a cycle if and only if it can be written
in the form
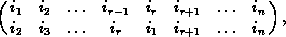 where r ³1.
In order to emphasize r we also call it an r-cycle .
We note that in this case the orbits of the subgroup generated by
this permutation are the following
subsets of n: {i1, ...,ir }, {ir+1 }, ..., {in }.
We therefore abbreviate
this cycle by (i1, ...,ir)(ir+1) ...(in),
where the points which are cyclically permuted are put together in
round brackets. For example
where r ³1.
In order to emphasize r we also call it an r-cycle .
We note that in this case the orbits of the subgroup generated by
this permutation are the following
subsets of n: {i1, ...,ir }, {ir+1 }, ..., {in }.
We therefore abbreviate
this cycle by (i1, ...,ir)(ir+1) ...(in),
where the points which are cyclically permuted are put together in
round brackets. For example
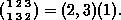 Commas which seperate the points may be omitted if no confusion
can arise (e.g if n £10), and 1-cycles can be left out if it is clear
which n is meant. Hence we can write p=(i1 ...ir) for the
r-cycle introduced above. This cycle p can also be expressed in
terms of i1
alone: p=(i1 pi1 ...pr-1i1). Using all these
abbreviations and denoting by 1:=(1) ...(n) the identity element,
we obtain for example
Commas which seperate the points may be omitted if no confusion
can arise (e.g if n £10), and 1-cycles can be left out if it is clear
which n is meant. Hence we can write p=(i1 ...ir) for the
r-cycle introduced above. This cycle p can also be expressed in
terms of i1
alone: p=(i1 pi1 ...pr-1i1). Using all these
abbreviations and denoting by 1:=(1) ...(n) the identity element,
we obtain for example
S 3= {1,(12),(13),(23),(123),(132) }.
There are the elements of the
symmetric group Sn
in cycle notation.
The notation for a cyclic permutation is not uniquely determined, since
(i1 ...ir)=(i2 ...ir i1)= ...=(ir i1 ...ir-1).
2-cycles are called transpositions .
The order
of a cycle
(i1 ...ir), i.e. the order of the cyclic group á(i1
...ir) ñ generated by this cycle, is equal to its length
:
| á(i1 ...ir) ñ | =r.
Two cycles p and r are called disjoint ,
if the two sets
of points which are not fixed by p and r are disjoint sets.
Notice that, for example, 1=(1)(2)(3) and (123) are disjoint cycles.
Disjoint cycles p and r commute, i.e. pr= rp.
(We read compositions of mappings from right to left, so that
( pr)x= p( rx).) Each permutation of a
finite set can be
written as a product of pairwise different disjoint cycles, e.g.
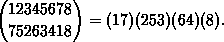 There are some more examples for the
cycle decomposition of a
permutation.
There are some more examples for the
cycle decomposition of a
permutation.
The disjoint cyclic factors not =1 of pÎSn are
uniquely determined by p and therefore we call these factors together
with the
fixed point
cycles of p the cyclic factors
of p.
Let c( p) denote the number of these cyclic factors of p
(including 1-cycles), let l n be their lengths, nÎ
c( p) (recall that c( p)= {1, ...,c( p) }),
choose, for each n an element j n of the n-th cyclic
factor. Then
p= Õ nÎ c( p)
(j n pj n ...pl n-1j n).
This notation becomes uniquely determined if we choose the j n so
that
" m Î N : j n
£pmj n, and
" n<c( p) : j n<j n+1.
If this holds, then the notation as was given above
is called the (standard) cycle notation
for p. We note in passing that the sets {j n, pj n,
..., pl n-1j n } of points which
are cyclically permuted by p
are just the orbits of the cyclic group ápñ generated
by p.
harald.fripertinger@kfunigraz.ac.at,
last changed: August 28, 2001
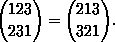 Keeping this in mind, we call a permutation pÎSn a cyclic
permutation or a cycle if and only if it can be written
in the form
Keeping this in mind, we call a permutation pÎSn a cyclic
permutation or a cycle if and only if it can be written
in the form
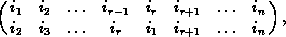 where r ³1.
In order to emphasize r we also call it an r-cycle .
We note that in this case the orbits of the subgroup generated by
this permutation are the following
subsets of n: {i1, ...,ir }, {ir+1 }, ..., {in }.
We therefore abbreviate
this cycle by (i1, ...,ir)(ir+1) ...(in),
where the points which are cyclically permuted are put together in
round brackets. For example
where r ³1.
In order to emphasize r we also call it an r-cycle .
We note that in this case the orbits of the subgroup generated by
this permutation are the following
subsets of n: {i1, ...,ir }, {ir+1 }, ..., {in }.
We therefore abbreviate
this cycle by (i1, ...,ir)(ir+1) ...(in),
where the points which are cyclically permuted are put together in
round brackets. For example
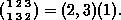 Commas which seperate the points may be omitted if no confusion
can arise (e.g if n £10), and 1-cycles can be left out if it is clear
which n is meant. Hence we can write p=(i1 ...ir) for the
r-cycle introduced above. This cycle p can also be expressed in
terms of i1
alone: p=(i1 pi1 ...pr-1i1). Using all these
abbreviations and denoting by 1:=(1) ...(n) the identity element,
we obtain for example
Commas which seperate the points may be omitted if no confusion
can arise (e.g if n £10), and 1-cycles can be left out if it is clear
which n is meant. Hence we can write p=(i1 ...ir) for the
r-cycle introduced above. This cycle p can also be expressed in
terms of i1
alone: p=(i1 pi1 ...pr-1i1). Using all these
abbreviations and denoting by 1:=(1) ...(n) the identity element,
we obtain for example
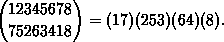 There are some more examples for the
cycle decomposition of a
permutation.
There are some more examples for the
cycle decomposition of a
permutation.