| Finite symmetric groups |
In the first section we mentioned the symmetric group SX on the set X. In order to prepare further examples and detailed descriptions of actions we need to consider this group in some detail, in particular for finite X. A first remark shows that it is only the order of X which really matters:
Lemma: For any two finite and nonempty sets X and Y, the natural actions of SX on X and SY on Y are isomorphic if and only if | X | = | Y | .
This is very easy to check and therefore left as an exercise. We call | X | the degree of SX, of any subgroup P £SX and of any pÎSX. In order to examine permutations of degree n it therefore suffices to consider a particular set of order n and its symmetric group. For technical reasons we introduce two such sets of order n:
n:= {0, ...,n-1 } and n:= {1, ...,n },
hoping that it will be always clear from the context if this set n is meant or its cardinality n.
It is an old tradition
to prefer the set n and its symmetric group which we should
denote by Sn in order to be consistent.
Hence let
us fix the notation for the elements of Sn , the corresponding
notation for
the elements of Sn is then obvious.
A permutation pÎSn is written down in full detail by putting the
images pi in a row under the points i În, say
 This will be abbreviated by
This will be abbreviated by
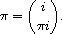 Hence, for example, S 3 consists of the following elements:
Hence, for example, S 3 consists of the following elements:
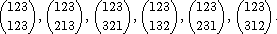 In our programs permutations will be written in the form [ p1, p2, ..., pn].
There is a program to
compute all elements of the symmetric group Sn .
In our programs permutations will be written in the form [ p1, p2, ..., pn].
There is a program to
compute all elements of the symmetric group Sn .
| harald.fripertinger "at" uni-graz.at | http://www-ang.kfunigraz.ac.at/~fripert/ | UNI-Graz | Institut für Mathematik | UNI-Bayreuth | Lehrstuhl II für Mathematik |
| Finite symmetric groups |