The point-hyperplane design on 15 points

The point-hyperplane design 2-(15, 7, 3)

One can construct a design by the incidence between points and hyperplanes of the projective geometry PG(3,2). In this design you have 15 points as well as 15 blocks. (hyperplanes). Every hyperplane contains 7 points and each pair of points is contained in exactly 3 hyperplanes.

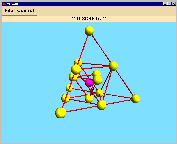
This design can be visualized by a tetrahedron:

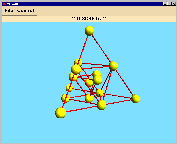
The steps of construction are the following:

First you take the vectors of weight 1 (0001, 0010, 0100 and 1000) as vertices of a tetrahedron. Then you can add every pair of these vertices, so you get 6 vectors of weight 2 and put them in the middle of the edges of the tetrahedron (this procedure gives an octahedron). The sum of 3 tetrahedron vertices gives the central point of the corresponding face (you get 4 of them; they form the dual tetrahedron of the original one). And last but not least you put the all-one vector 1111 right into the middle of the tetrahedron.


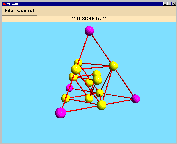
First you take the vectors of weight 1 (0001, 0010, 0100 and 1000) as vertices of a tetrahedron.	Then you can add every pair of these vertices, so you get 6 vectors of weight 2 and put them in the middle of the edges of the tetrahedron (this procedure gives an octahedron).	The sum of 3 tetrahedron vertices gives the central point of the corresponding face (you get 4 of them; they form the dual tetrahedron of the original one).	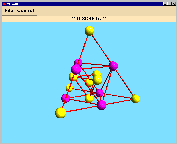And last but not least you put the all-one vector 1111 right into the middle of the tetrahedron.

The "recipe" for the group selection "solids" in DISCRETA is the following:

take a tetrahedron
take the edge midpoints of the tetrahedron (by pressing "Tetrahedron", "choose", "midpoints of edges" and again "choose") - this gives an inscribed octahedron
take the dual (which is also a tetrahedron, whose vertices are the midpoints of the faces of the original tetrahedron) by pressing "Tetrahedron", "choose", "dual" and "choose"
last thing to do is to choose "add central point"

The results of each single step is coloured in pink at the pictures above.

This construction yields a group derived from the symmetry group A_4 (group order: 12) of the tetrahedron (the group is induced on the edge midpoints and on the dual tetrahedron, and finally you can add a fixpoint such that you get a group on 15 points). Under the action of this group you receive by computations with DISCRETA 6 2-(15, 7, 3) designs (some of them are isomorphic under a larger group). More information on them you can read in this report.

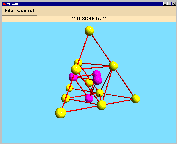
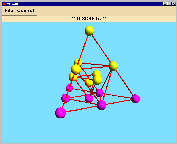
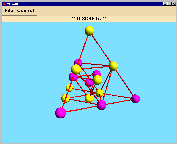
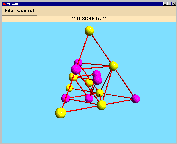
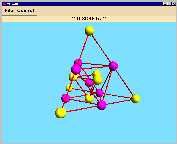
One of the designs is visualized below: you get the following orbit representants coloured in pink (with the corresponding orbit length). Adding the orbit lengths, we get 15 blocks as recommended.

orbit length: 4 orbit length: 6 orbit length: 4 orbit length: 1



orbit length: 4	orbit length: 6	orbit length: 4	orbit length: 1

The projective geometry PG(3,2):

When we consider the 2-subsets and the 3-subsets of the 15 points above and fix lambda=1, we receive the following Kramer-Mesner matrix w.r.t. the action of the same group(size: 13x46):

3 3 1 3 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 3 1 0 0 3 3 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 2 2 0 2 2 4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 2 1 2 2 1 2 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 0 1 2 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 0 0 2 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 3 0 0 0 0 3 0 0 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 0 0 0 0 1 1 1 0 0 1 1 1 1 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 4 0 0 0 0 0 0 0 0 0 0 0 0 2 0 2 0 0 0 0 4 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 1 2 1 0 1 1 1 1 0 0
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 1 0 1 2 1 0 1 1 1 0
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 0 0 0 0 0 0 0 0 0 1 2 2 1 2

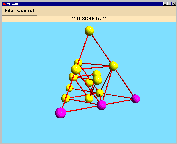
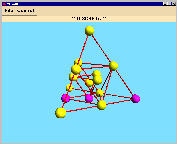
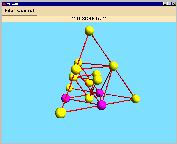
It is very interesting that we can visualize the projective plane PG(3,2) with this construction of the tetrahedron - it is a Steiner triple system on 15 points. By solving the corresponding matrix equation, one gets 12 designs with DISCRETA, the orbits of one of them are the following (see also the report):

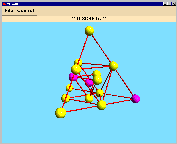
orbit length: 6 orbit length: 12 orbit length: 4

orbit length: 4 orbit length: 6 orbit length: 3



orbit length: 6	orbit length: 12	orbit length: 4

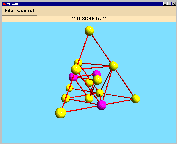
orbit length: 4	orbit length: 6	orbit length: 3

Therefore we get 35 blocks. It is a very interesting remark that all the blocks of the point-hyperplane design above consist of Fano planes whose blocks are exactly blocks from the PG(3,2)!

To the DISCRETA homepage.

Back to the homepage of Evi Haberberger.

To the homepage of Lehrstuhl II.

Last updated: June 16, 1999.