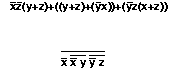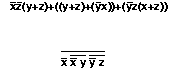Prof. Dr. R. Laue WS0001 Informatik I
Übungsblatt 6
Abgabe: 30.11.00 vor der Vorlesung

URL: /axel/informatik1_ws0001_blatt6.html
Dieses Übungsblatt ist in Zweiergruppen zu bearbeiten. Auf dem Blatt bitte den Übungsgruppentag angeben. Um den Übungsschein zu erhalten, muß man 50% der Punkte erreichen und zweimal erfolgreich eine Aufgabe vorrechnen.

Aufgabe 17 - 7-Segmentanzeige - (6 Punkte)

In der Vorlesung wurde die 7 Segmentanzeige durch die Funktionen a,b,c,...,g beschrieben. Man stelle die Funktion b mittels Quine Mc Cluskey in möglichst kurzer disjunktiver Form da. (4 Punkte) Wie kann man durch geschickte Wahl der Funktion b auf den überflüssigen Punkten 1010,...,1111 erreichen, daß die Terme kurz werden. (2 Punkte)

Aufgabe 18 - disjunktive Normalform - (3 Punkte)

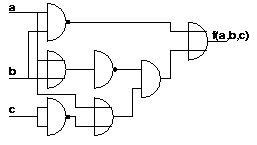
Geben Sie die Funktion f(a,b,c) in kanonischer disjunktiver Normalform an. Kreuzungen im Schaltungsbild sind ohne Verbindung.

Aufgabe 19 - konjunktive Normalform - ( 2+2 Punkte)

Zeigen Sie indem Sie in konjunktive Normalform transformieren, daß die beiden Terme

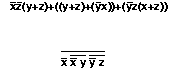
dieselbe Funktion definieren.

Aufgabe 20 - EXOR , Halbaddierer (1+3+1 Punkte)

Der EXOR Baustein ist neben NAND, ODER, NICHT, UND ein weiterer Baustein um Schaltnetze zu erstellen. Man definiert:

EXOR(x,y) = 0 falls x=y
EXOR(x,y) = 1 sonst

Ein weiterer Baustein ist der Halbaddierer mit zwei Eingängen x,y und einem Ausgang ü, der den Übertrag enthält und einem Ausgang s mit der (natürlich einstelligen) Summe von x und y.

a) Drücken Sie EXOR mittels +,^. und Negation aus.
b) Drücken Sie EXOR mit Hilfe von 4 NAND Gattern dar. Zeichnen Sie das zugehörige Schaltbild
c) Drücken Sie s und ü mit Hilfe von^. und EXOR aus, zeichen Sie das Schaltbild des Halbaddierers.