Prof. Dr. R. Laue                                                                            WS0203
                                Graphentheoretische Optimierung
                                Übungsblatt 8
Abgabe: bis Donnerstag 12.12.02 12.00 Raum 736 Mathe NW2

URL:         /axel/graph_ws0203_blatt8.html
 

Aufgabe 16- bcc Teil 2 - (6+2 Punkte)


Auf unserem Weg zum Algorithmus für bcc beweisen wir zwei weitere Aussagen:

Sei G=(V,E) ein ungerichteter Graph ohne Schleifen. Seien T,F,B,DFSNUM,FATHER, LOWPR wie in Aufgabe 15 definiert.

Es gilt:

1) Sei G'=(V',E') ein bcc von G mit Zentrum v. Dann ist

            V'={FATHER[v] union w; wobei für w gilt: es ex ein Weg von v nach w mit Kanten aus T und kein Knoten ausser v auf  diesem  Weg ist Zentrum}
 

2) Es gilt:  LOWPT[v] = min(
                            { DFSNUM[v] } union
                            { DFSNUM[z] mit (v,z) 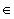 B}  union
                            { LOWPT[u] mit (v,u) 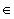 T}
                                            )
     für alle v aus V
 

Aufgabe 17 bcc - letzter Teil - (4 + 2 Punkte)


Ändern Sie den Algorithmus für die starke Zusammenhangskomponente so ab, dass die Zweifachzusammenhangskomponenten berechnet werden. Warum funktioniert der Algorithmus? Führen Sie ein instruktives Beispiel vor.