Prof. Dr. R. Laue
WS0203
Graphentheoretische Optimierung
Übungsblatt 11
Abgabe: bis Donnerstag 23.1.03 12.00 Raum 736 Mathe NW2
URL:
/axel/graph_ws0203_blatt11.html
Aufgabe 22 Ford Fulkerson (3 Punkte)
Man konstruiere ein Beispiel mit einem Blocking Flow, der nicht der
maximale Fluss ist.
Aufgabe 23 Wir helfen der NASA - (5+3 Punkte)
(nach Ross)
Ein Raumschiff soll zu einem entfernten Planeten aufbrechen. Der Flightmanager
muss entscheiden welche der m möglichen Ausrüstungsgegenstände
Ai an Bord genommen werden soll. Jeder Ausrüstungsgegenstand
verursacht Kosten ci (natürlich >0). Mit den Ausrüstungsgegenständen
kann man aber Experimente Ej durchführen. Jedes Experiment
der insgesamt n möglichen bringt einen Gewinn von gj (wieder
>0). Für jedes Experiment ist eine Teilmenge der Menge aller Ausrüstungsgegenstände
nötig. Der Flightmanager muss nun den Gesamtertrag der Mission maximieren,
d.h. er muss Ausrüstungsgegenstände so auswählen, dass die
Summe über die Erträge der Experimente abzüglich der Summe
über die Kosten der Ausrüstungsgegenstände maximal wird.
Wie kann hier max flow / min cut helfen?
Lösen Sie folgendes Problem:
Es gibt 5 Ausrüstungsgegenstände zu Kosten (c1= 4,c2=5,c3=7,c4=1,c5=2)
.
Experiment 1 bringt 3 Einheiten Gewinn und benötigt Ausrüstungsgegenstände
1 und 2.
Experiment 2 bringt 8 Einheiten Gewinn und benötigt Ausrüstungsgegenstände
3 und 2.
Experiment 3 bringt 6 Einheiten Gewinn und benötigt Ausrüstungsgegenstände
3, 4 und 2.
Experiment 4 bringt 3 Einheiten Gewinn und benötigt Ausrüstungsgegenstände
4 und 5.
Welche Ausrüstungsgegenstände soll der Flightmanager an Bord nehmen?
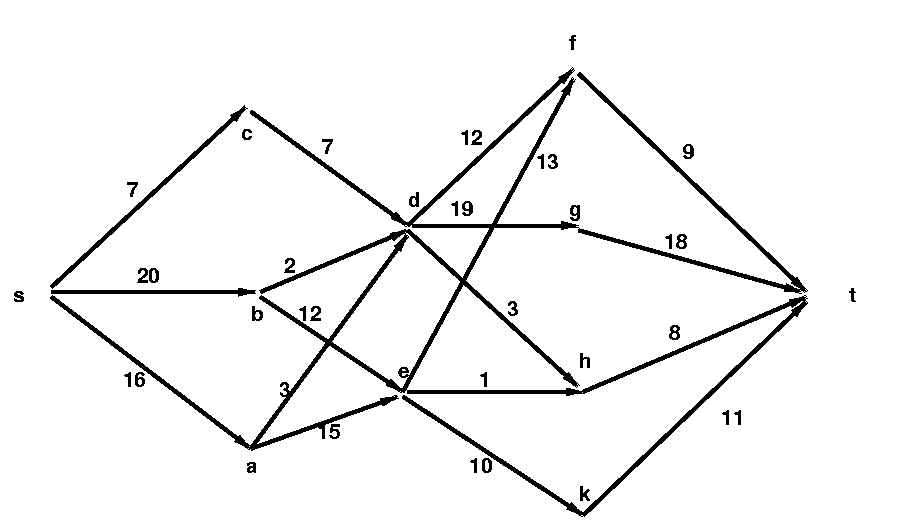
Aufgabe 24 Blocking Flow - (4+4 Punkte)
In der Vorlesung wurde das Verfahren von Malhotra,Kumar, Mahaswari
zur Berechnung eines 'blocking flow' mit Aufwand O(|V|2) vorgestellt.
1) Formulieren Sie es als Algorithmus in Pseudocode.
2) Berechnen Sie einen blockierenden Fluss für folgendes geschichtete
Netzwerk (aus Syslo,Deo, Kowalik)